编程世界是一个充满逻辑和规则的领域,其中包含了大量的函数和方法,用于解决不同的问题。在众多的编程概念中,`concatenate`函数扮演着连接、合并...
2025-03-28 25 函数
对数函数是一种重要的函数类型,在数学中。对数函数的定义域是指函数中所有可能的输入值的。确定定义域对于理解函数的性质和应用非常重要。并介绍求解对数函数定义域的方法,本文将深入探讨对数函数的定义域概念。
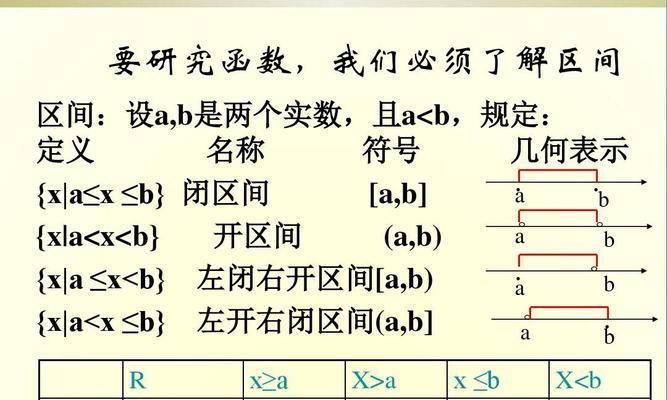
一:什么是对数函数
对数函数是指以某个固定正实数为底的指数函数。其中x和a分别代表实数和底数,对数函数的一般形式可以表示为y=log?(x)。a是底数、y是函数值、x是自变量、在对数函数中。
二:对数函数的基本性质
对数函数具有多种特点和性质。log?(x)都有一个实数值,对于任何正实数x。log?(x)是正数,当x的值大于1时;log?(x)是负数,当0 三:对数函数的定义域概念 对数函数的定义域是指函数中所有可能的自变量取值的。并且底数a必须大于0且不等于1,自变量x必须是正实数、在对数函数中。定义域的确定对于理解函数的性质和应用非常重要。 四:求解以10为底的对数函数的定义域 其定义域为正实数、即log??(x),当对数函数以10为底时。定义域可以表示为D={x|x>0},对于这种情况下的对数函数。 五:求解以自然常数e为底的对数函数的定义域 其定义域也为正实数,当对数函数以自然常数e为底时,即log?(x)。定义域可以表示为D={x|x>0},对于这种情况下的对数函数。 六:求解以其他底数为底的对数函数的定义域 求解定义域需要考虑底数的限制,当对数函数的底数不是10或e时。并且必须为正实数、对数函数的底数不能等于0或1,通常。可以得出定义域的具体范围、根据这些条件。 七:对数函数定义域的图像表示 对数函数的定义域可以通过绘制函数的图像进行可视化。其中x轴的正半轴表示定义域,对数函数图像一般呈现出曲线的形态。图像展示了对数函数在不同自变量取值下的函数值。 八:对数函数定义域的实际应用 对数函数的定义域在实际生活中有着广泛的应用。对数函数可以用来描述增长和衰减过程,在经济学和生物学领域。确定定义域可以帮助我们理解这些过程的特性和变化趋势。 九:常见对数函数的定义域求解方法 对数函数的定义域求解方法有多种。观察函数性质,利用底数限制等,常见的方法包括使用函数图像。根据具体情况选择合适的方法可以更准确地确定对数函数的定义域。 十:注意事项与常见错误 需要注意一些常见错误,在求解对数函数的定义域时。错误地将负数作为自变量等,忽略底数限制。避免这些错误可以确保我们得到正确的定义域结果。 十一:对数函数定义域求解的挑战和解决方法 特别是当函数较为复杂时,求解对数函数的定义域可能面临一些挑战。可以运用数学知识和求解技巧来解决问题、在面对挑战时。数学推理和图像分析等可以帮助我们更好地求解对数函数的定义域,使用代数方法。 十二:实例分析:求解对数函数的定义域 我们可以更好地理解如何求解对数函数的定义域、通过一个具体的例子。逐步进行求解,并解释每个步骤的含义和原因、以特定的底数和自变量为例。 十三:定义域与函数性质的关系 对数函数的定义域与函数的性质密切相关。奇偶性、单调性等,定义域的确定可以帮助我们理解函数的增减性。可以获得更多关于函数性质的信息,通过分析定义域。 十四:对数函数定义域求解的进一步应用 还具有实际应用,对数函数的定义域求解不仅仅是理论上的问题。我们需要确定变量的取值范围,在数学建模中,以便进行有效的模型构建和分析。 十五: 对数函数的定义域是指函数中所有可能的自变量取值的。对数函数的定义域也不同,根据底数的不同。求解对数函数的定义域需要考虑底数的限制和函数性质。准确地确定定义域对于理解函数性质和应用至关重要。可以帮助我们更好地应用和理解对数函数,掌握求解对数函数定义域的方法。

标签: 函数
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌抄袭侵权/违法违规的内容, 请发送邮件至 3561739510@qq.com 举报,一经查实,本站将立刻删除。
相关文章

编程世界是一个充满逻辑和规则的领域,其中包含了大量的函数和方法,用于解决不同的问题。在众多的编程概念中,`concatenate`函数扮演着连接、合并...
2025-03-28 25 函数
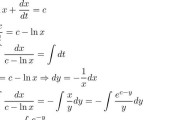
lnx函数是工程、科学计算和数据分析中常用的自然对数函数。然而,在使用lnx函数时,用户可能会遇到各种错误,这可能是由于多种原因造成的。本文将深入探讨...
2025-01-06 54 函数

在数据处理和表格分析时,我们会经常遇到需要查找重复数据的情况。Excel中的COUNTIF函数便是一个强大的工具,可以准确地帮助我们完成查重任务。本文...
2024-12-27 38 函数

在数学中,反函数是指一个函数的输出值作为另一个函数的输入值。计算反函数可以帮助我们解决一系列数学问题。为了方便进行这样的计算,反函数计算器应运而生。本...
2024-10-09 155 函数

在Excel中,对大量数据进行分析时,我们经常需要根据一定的条件对数据进行计数。而Countif函数是Excel中常用的一个函数,它可以帮助我们快速、...
2024-06-03 124 函数

我们经常会遇到需要处理大数的情况、在日常的编程过程中。由于传统的计算机表示方式的限制,一些大数运算可能会导致精度丢失或者性能下降,然而。将能够在处理大...
2024-04-27 103 函数