用微积分推导圆的面积公式（三种微积分方式解析圆的面积推导）

解决许多实际问题，它可以应用于各个领域、微积分是数学中的重要分支。我们将探讨如何利用微积分的三种方法推导圆的面积公式，在本文中。我们可以更深入地理解微积分的原理与应用、通过这些推导。

一、定积分的几何解释

1.1定积分的概念及几何意义

定积分可以看作是一个曲线下面积的求和。并通过定积分求和的方式求得整个圆的面积，在推导圆的面积公式中，我们可以将圆弧细分成无数个小扇形。

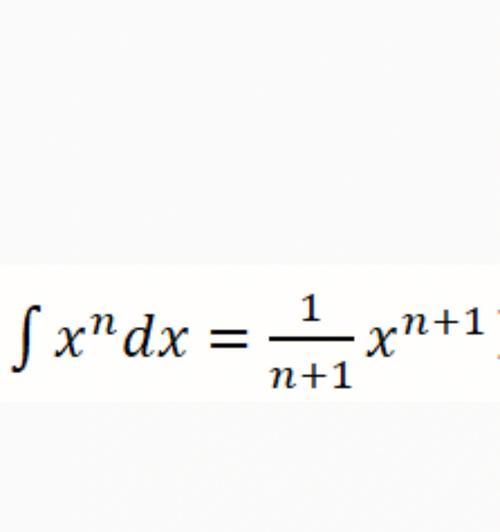
二、极坐标系下的面积计算

2.1极坐标系下圆的方程

我们可以更方便地描述圆，并得到其方程，利用极坐标系。可以推导出圆的面积公式，通过对极坐标下圆形区域进行面积计算。

三、变量代换法的应用

3.1变量代换法的基本概念

可以通过变换自变量的方式简化问题，变量代换法是微积分中常用的一种方法。并最终得到面积公式，在推导圆的面积公式中，我们可以通过变量代换将原本的圆形区域变换为更易计算的形式。

四、积分的展开与奇偶性

4.1奇偶函数的性质

奇函数和偶函数在微积分中具有一些特殊的性质。我们可以对圆的面积公式进行展开、并简化计算过程，利用这些性质。

五、微分方程与面积公式推导

5.1微分方程与曲线的面积

可以描述曲线的特征，微分方程是微积分中的重要工具。我们可以得到圆的面积公式、通过解微分方程并结合面积概念。

六、比较不同推导方法的优劣

6.1各种推导方法的优缺点

我们将比较三种微积分方式推导圆的面积公式的优劣，在本节中。我们可以了解每种方法的适用范围和计算复杂度，通过对比分析，选择最适合自己的方法。

七、实际应用案例：

7.1基于微积分的面积计算实例

我们将应用前面推导的圆的面积公式，并验证其正确性，通过实际的面积计算案例。这将帮助我们更好地理解微积分在实际问题中的应用。

八、推导过程中的注意事项

8.1推导过程中需要注意的问题

我们需要注意一些细节和特殊情况，在推导圆的面积公式时。帮助读者避免常见错误，本节将提供一些推导过程中需要注意的事项。

九、推导结果的证明与讨论

9.1推导结果的证明与合理性分析

并进行合理性分析，在本节中，我们将对推导得到的圆的面积公式进行证明。我们可以确保推导结果的正确性，通过论证与讨论。

十、拓展与应用：其他曲线的面积计算

10.1其他曲线面积计算的思路

我们可以推广到其他曲线形状的面积计算，通过对圆的面积推导。计算其他曲线的面积、本节将介绍如何应用微积分的思想。

十一、

我们深入了解了微积分在推导圆的面积公式中的应用，通过本文的探讨。都为我们提供了不同的思路和方法，还是极坐标系，变量代换法以及微分方程的应用，无论是定积分的几何解释。也为我们今后解决更多实际问题提供了思路和启示，这些推导过程不仅展示了微积分的强大魅力。